Знакомство с GNU Octave

GNU Octave открытое ПО для математических расчетов, известное тем, что поддерживает совместимость с коммерческим MATLAB на очень высоком уровне, фактически это клон MATLAB, т.к. даже малейшая несовместимость рассматривается разработчиками как ошибка.

Первоначально Octave был разработан в качестве сопутствующего программного обеспечения для учебного курса для студентов по проектированию химических реакторов. Позже главный разработчик J.W. Eaton переделал полностью законченный продукт и теперь он активно используется как на производстве, так и в академических целях. Особенно часто Octave используют для матричных вычислений и это имеет смысл, т.к. большая часть инженерных задач и представление данных чаще всего требуют векторного и матричного подхода.

Почему именно Octave? Есть очень много языков программирования, к примеру C, Python, Java, которые позволяют решать подобные задачи, но когда дело доходит до стадии прототипирования и разработки концепции, основным требованием является скорость реализации, то есть время, необходимое для реализации алгоритма. И MATLAB, и Octave как раз созданы для решения проблем такого рода, выполнения вычислений и выдача результата на дисплей.

Octave обладает обширными инструментами для решения общих задач численной линейной алгебры, нахождения корней нелинейных уравнений, интегрирования обычных функций, манипулирования полиномами и интегрирования обыкновенных дифференциальных и дифференциально-алгебраических уравнений. Он легко расширяем пользовательскими функциями, которые можно писать на собственном языке данной программы или, используя динамически загружаемые модули, написанные на C/C++, Fortran и других языках.

Варианты использования:

Исследование и разработка концептов на производстве и в академических целях.
Получение похожего по функционалу на MATLAB софта, но бесплатно.
Разработка и тестирование математических алгоритмов.

Например,

NASA использует Octave для разработки систем стыковки космических аппаратов.
Jaguar анализирует данные, получаемые от их болидов Formula 1.
Шеффилдский Университет использует Octave для разработки программного обеспечения для распознавания раковых клеток.

Как видите, применений данной программы может быть множество и она безусловно позволяет писать программы быстро, а также визуализировать данные во множестве сфер и направлений. Лично для меня этот пакет интересен в рамках моих задач по цифровой обработке радиочастотных сигналов, которую я начал изучать.

Установить программу довольно просто. Текущая версия 5.1.0 и самый простой вариант ее получения, если у вас конечно Linux, это установка через flatpak командой flatpak install flathub org.octave.Octave. Как там обстоят дела с другими дистрибутивами и операционными системами можно узнать на официальном wiki.

Простые примеры

Рассмотрим несколько простых примеров, чтобы максимально быстро войти в курс дела и понять как все тут работает. Взято с документации.

Элементарные вычисления

Octave поддерживает следующие арифметические операции + - * /, возведение в степень ^, натуральные логарифмы/показатели (log, exp), тригонометрические функции (sin, cos, …). Кроме этого, Octave может работать как с вещественными числами, так и с комплексными (i, j). Также предопределены некоторые математические константы, например, число pi и основание натурального логарифма e.

Попробуем для начала проверить тождество Эйлера.

Из Википедии
Известное тождество, связывающее 5 фундаментальных математических констант.

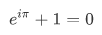
Вводим в командное окно следующее выражение:

>> exp(i*pi)

Ответ должен быть равен -1, я у себя получил следующее:

ans = -1.0000e+00 + 1.2246e-16i

Создание матриц

Векторы и матрицы базовые строительные блоки числового анализа. Для создания матрицы и сохранения ее в переменную для последующего использования нужно ввести следующую команду:

>> A = [ 1, 1, 2; 3, 5, 8; 13, 21, 34 ]

И получим ответ:

A =
    1    1    2
    3    5    8
   13   21   34

Если ввести команду, поставив в конце точку с запятой, то Octave не будет выводить матрицу на экран, например, создадим матрицу на 3 строки и 2 столбца со случайными числами:

>> B = rand (3, 2);

Теперь для того, чтобы получить вывод данной матрицы на экран, достаточно ввести в командное окно имя переменной, в которой она сохранена:

>> B

Арифметика матриц

Умножение матрицы на скаляр:

>> 2 * A

Перемножение двух матриц:

>> A * B

Умножение транспонированной матрицы на саму себя:

>> A' * A

Решение систем линейных уравнений

Разберем на примере следующего уравнения

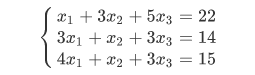
Распишем матрицы коэффициентов и свободных членов для этой системы уравнений

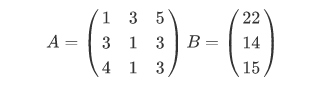
Теперь набираем обе получившиеся матрицы в Octave и решаем систему методом наименьших квадратов с помощью, так называемого оператора левого деления \

>> A = [1 3 5; 3 1 3; 4 1 3];
>> B = [22; 14; 15];
>> A\B
ans =
   1.0000
   2.0000
   3.0000

Решение нелинейных дифференциальных уравнений

Octave может проинтегрировать уравнения следующего вида

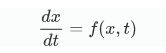
Пробуем ввести функцию в Octave, сделать это несложно, гораздо сложнее понять, что ты только что сделал) Я уже давно забыл всю теорию вышмата, так что просто повторил пример и это работает, позже уже буду разбираться как.

>> function xdot = f (x, t)

r = 0.25;
k = 1.4;
a = 1.5;
b = 0.16;
c = 0.9;
d = 0.8;

xdot(1) = r*x(1)*(1 - x(1)/k) - a*x(1)*x(2)/(1 + b*x(1));
xdot(2) = c*a*x(1)*x(2)/(1 + b*x(1)) - d*x(2);

endfunction
>> x0 = [1; 2];
>> t = linspace (0, 50, 200)';
>> x = lsode ("f", x0, t);

Последняя команда производит интегрирование и если ее выполнить без ; в конце, то можно будет увидеть много цифр рассчитанной функциональной зависимости.

Графический вывод

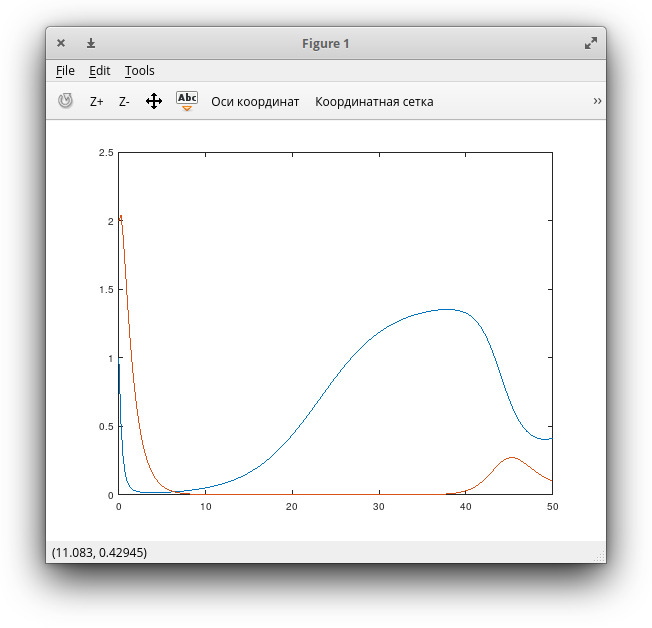
Чтобы получить график, полученного в прошлом примере решения достаточно ввести команду:

>> plot (t, x)

Octave тут же создаст новое окно с вот таким вот красивым графиком, который к тому же можно сохранить скажем в pdf формат командой:

>> print -dpdf ~/foo.pdf

Пока на этом все, буду стараться использовать Octave в разработке и если у меня будет получаться, то я непременно напишу об этом в блоге. А пока подписывайтесь куда-нибудь (ВК, Твиттер), что-нибудь жмите, что-нибудь пишите (Телеграм). Всем пока!