Данная статья полностью теоретическая и является прологом для последующих, в которых я постараюсь сделать небольшое исследование в области субдискретизации узкополосных высокочастотных сигналов и их цифровой обработки. Я не эксперт в области цифровой обработки сигналов, а только учусь), так что пока постараюсь обойтись без сложных формул, они будут в следующей статье.
Сразу дадим определение:
Субдискретизация
процесс дискретизации сигнала, находящегося вне первой зоны Котельникова-Найквиста.
Чтобы понять, что такое субдискретизация, нужно для начала понять, что такое собственно дискретизация, что такое зоны Котельникова-Найквиста, что происходит в процессе дискретизации и где это может использоваться. Начнем понемногу.
О дискретизации
Дискретизация
это определение значений непрерывного сигнала (например, аналогового) в дискретные моменты времени.
По теореме о дискретном представлении, чтобы выборки полностью описывали сигнал, дискретизация должна осуществляться на частоте:
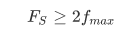
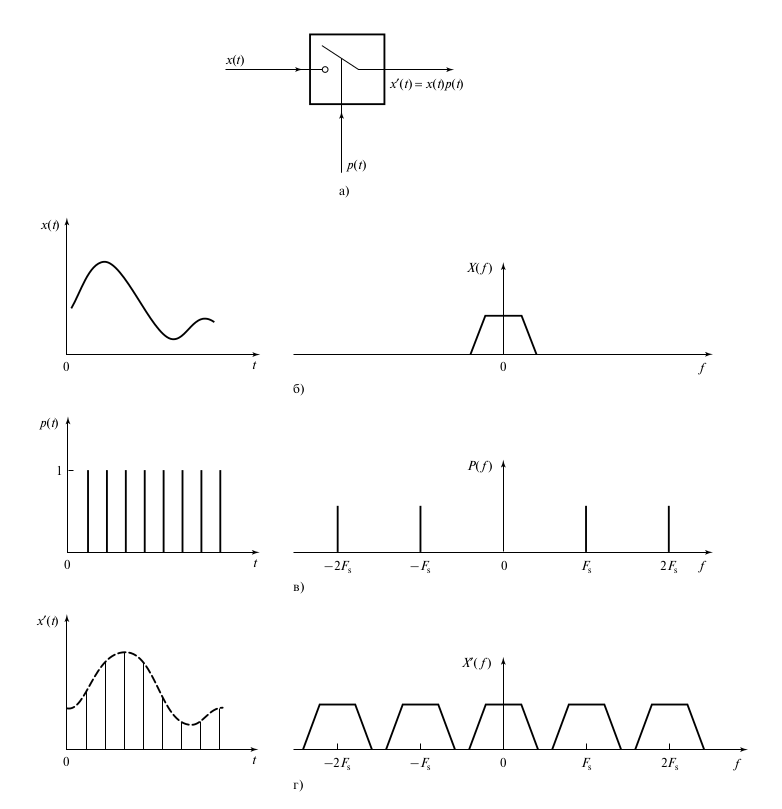
На рисунке ниже показан процесс дискретизации, который можно рассматривать как умножение аналогового сигнала x(t) на выборочную функцию p(t). Функция p(t) состоит из импульсов единичной амплитуды бесконечно малой длительности и периодом T. На рисунке также показаны спектры сигналов. X'(f) — это свертка X(f) и P(f), следовательно умножение во временных координатах экививалентно свертке в частотных координатах.
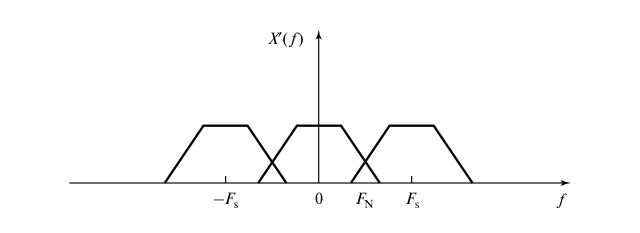
Можно увидеть как отличаются спектры сигнала до (б) и после (г) дискретизации и можно заметить, что спектр дискретного сигнала повторяется в точках, кратных частоте дискретизации Fs.
Про дискретный сигнал можно отметить следующие моменты:
- Спектр идентичен исходному аналоговому сигналу, только повторяется в точках кратных частоте дискретизации Fs, т.е. появляются зеркальные частоты.
- При небольшой частоте дискретизации, зеркальные частоты будут накладываться на частоты основной полосы и не будет возможности восстановить исходный аналоговый сигнал из дискретного.
- Наложение происходит в точке Fn, равной половине частоты дискретизации, эту точку называют частотой Котельникова-Найквиста. Таким образом, мы получаем зоны Котельникова-Найквиста, в которых появляются образы сигнала, ограниченные половиной частоты дискретизации.
На практике наложение присутствует всегда, из-за шума и наличия сигналов за пределами полосы частот полезного сигнала, следовательно главная задача разработчика создать подходящий фильтр для защиты от наложения спектров, обеспечивающий достаточное подавление (с учетом разрешающей способности АЦП) на частотах, превышающих частоту Котельникова-Найквиста, а также выбрать подходящую частоту дискретизации.
Более подробно описывать фильтрацию от наложения спектра я не буду, т.к. это выходит за пределы темы статьи. Кому интересно, найдет данную информацию в книгах или может почитать тут про антиалайзинговый фильтр. Также опущу факторы, которые влияют на выбор частоты дискретизации, это тема для отдельной статьи, которая будет позже.
О субдискретизации
Часто бывает, что, например, в системах связи, полезный сигнал занимает только узкую часть доступной полосы частот. Это относится к дискретизации сигнала на промежуточной частоте в приемниках. Выше мы рассматривали случаи дискретизации низкочастотных сигналов, которые полностью находятся в первой зоне Котельникова-Найквиста. На следующем рисунке показан случай, когда полоса частот полезного сигнала ограничена первой зоной дискретизации, а на выходе дискретизатора в остальных зонах появляются образы полезного сигнала, как уже об этом говорилось выше.
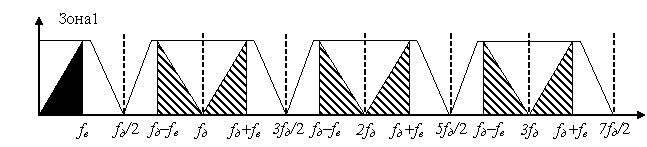
Теперь взглянем на случай, когда полоса сигнала находится во второй зоне Котельникова-Найквиста.
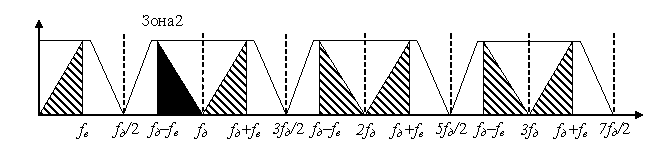
Именно такая ситуация возникает при обработке сигнала радиоприемника, где сигнал переносится на промежуточную частоту и гарантируется, что сигнал за пределами полосы пропускания фильтра промежуточной частоты отсутствует. Дадим еще раз определение субдискретизации:
Субдискретизация
процесс дискретизации сигнала, находящегося вне первой зоны Котельникова-Найквиста.
Образ сигнала в первой зоне Котельникова-Найквиста содержит всю информацию об исходном сигнале, кроме его первоначального положения на оси частот. Для четных зон Котельникова-Найквиста, порядок частот в спектре образа сигнала в первой зоне обратный и это следует учитывать при обработке.
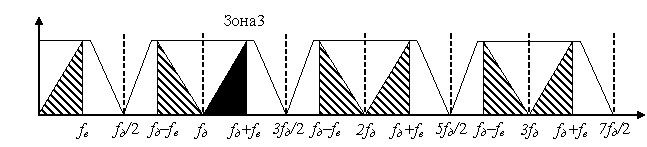
Рассмотрим образ сигнала в третьей зоне Котельникова-Найквиста, здесь уже на выходе дискретизатора в первой зоне, обращения частот не происходит. Таким образом, полоса частот сигнала, подлежащая дискретизации может лежать в любой зоне Котельникова-Найквиста и сигнала в первой зоне является точным образом исходного сигнала, за исключением обращения частот, которое проиходит в четных зонах Котельникова-Найквиста. Дадим еще одну формулировку:
Определение
Сигнал должен быть дискретизирован со скоростью равной или большей удвоенной полосы частот полезного сигнала для того, чтобы сохранить всю информацию об исходном сигнале.
В данной формулировке нет никакого упоминания о положении сигнала в частотном спектре относительно частоты дискретизации, главное, чтобы он был ограничен одной зоной Котельникова-Найквиста и его частотные компоненты не должны выходить за частоту Fs/2, что является задачей для антиалайзингового фильтра, который размещается до аналого-цифрового преобразователя.
Данная техника дискретизации используется в приемной аппаратуре, как я уже писал выше. Процесс эквивалентен аналоговой демодуляции с последующей цифровой обработкой сигнала. Это позволяет избавиться от демодулятора промежуточной частоты, однако накладывает определенные требования на производительность АЦП, который должен работать в более высокочастотных зонах Котельникова-Найквиста и вносить минимальные искажения во входной сигнал, именно такие АЦП используются для субдискретизации.
В следующей статье из данной серии рассмотрим некоторые практические примеры выбора частоты дискретизации, что-нибудь посчитаем, попробуем задействовать для этих целей GNU Octave, о котором я уже писал ранее. А пока подписывайтесь на обновления блога в Твиттер и ВК, а также заходите в наш чат Телеграм.
Использованные источники:
- Айфичер Э., Джервис Б. — Цифровая обработка сигналов. Практический подход (изд.2), 2008 г.
- Статья «Дискретизация сигнала на промежуточной частоте (субдискретизация)», 2013 г.
- Солонина А. Цифровая обработка сигналов в зеркале MATLAB, 2018 г.